0x00 神经网络简介
神经网络最早能追溯到上世纪40年代的MP模型,而上世纪80年代的误差反向传播算法(BP算法),神经网络得以进一步发展,研究者开始增加网络层实现非线性功能,但由于那时计算机的计算能力非常弱,其发展一度陷入了停滞。直到2006年,Hinton提出深度信念网络(DBN),由于当时计算机计算能力有所提升,该算法能够提供更好的策略来训练模型,深度学习迎来新的生机。在图像识别领域,深度学习方法的引入打破了传统模式识别方法识别效能的瓶颈。2012年ImageNet比赛,冠军是基于CNN网络的模型AlexNet,而基于SVM方法的模型却夺得亚军。这场比赛的结果昭示了神经网络在图像识别领域的巨大前景,也揭开了深度图像识别新的研究方向。下面会介绍神经网络的基本结构,并概括分析现有的深度学习网络。
0x10 神经网络基本概念
0x11 神经元
正如生物学中的概念,计算机科学中神经网络的神经元是最基本的构件。它的功能跟人的神经元类似,即:给定一些输入给神经元,它会产生输出。从数学的角度出发,神经元就是一个数学函数,它能根据输入结合函数的性质,计算出结果并输出。如图:
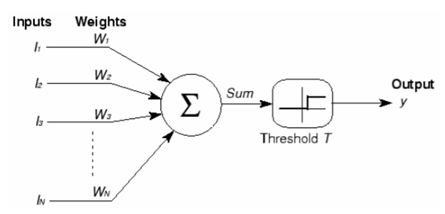
不同神经元由不同的函数构成,这些函数在术语上称为激活函数。下面会介绍几种常见的激活函数。
0x12 激活函数
阶跃函数
阶跃函数的定义如下: \[ f(x)=\left\{\begin{array}{ll}{0} & {\text { for } x<0} \\ {1} & {\text { for } x \geq 0}\end{array}\right. \tag{1} \] 其函数图如下图:
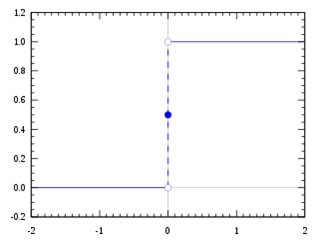
根据公式\((1)\)可知,如果x的值大于或等于0,输出为1;否则,输出为0。由图4.2可知阶跃函数在零点是不可微的。而梯度下降法常用于神经网络反向传播模型中,其思想是多变量微分寻找极值点,所以梯度下降法不能利用阶跃函数微分,所以研究者需要找到一个能够可微的替代函数,Sigmoid函数由此产生。
Sigmoid函数
Sigmoid函数定义如下: \[ f(x)=\sigma(x)=\frac{1}{1+e^{-x}} \tag{2} \] 其函数图如下图:

根据公式\((2)\)可知,当自变量z趋于负无穷或正无穷时,函数的值趋于-1或1。它是有界可微函数,并且在函数的每个点都有一个正导数。由于其可微性,通常被用于反向传播模型中的梯度下降法中。
Tanh函数
Tanh函数定义如下: \[ \tanh x=\frac{\sinh x}{\cosh x}=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \tag{3} \] 其函数图如下图:

由公式\((3)\)可知,Tanh函数其实就是Sigmoid函数因变量的取值范围从\([0,1]\)变成\([-1,1]\),它是一个基本的双曲函数。如Sigmoid函数,Tanh函数是可微的、单调递增的函数。与Sigmoid函数不同的是:当输入为负数时,\(\tanh\ x\)值为负数;输入为0时,\(\tanh\ x\)值为0。所以Tanh函数常用于分类器中。
ReLU函数
ReLU函数定义如下: \[ f(x)=\left\{\begin{array}{ll}{0} & {\text { for } x<0} \\ {1} & {\text { for } x \geq 0}\end{array}\right. \ or \ \mathrm{R}(x)=\max (0, \mathrm{x}) \tag{4} \] 其函数图如下图:
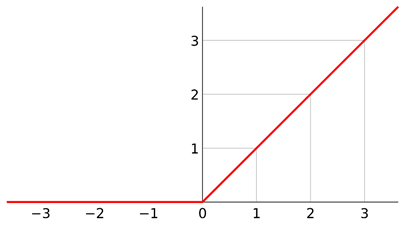
由公式\((4)\)可知,ReLU自变量小于0时因变量恒为0,大于0时自变量等于因变量。ReLU是目前研究中,使用最频繁的激活函数,它通常被用在CNN或DL(Deep Learning)中。
下图显示了比较常用的激活函数:
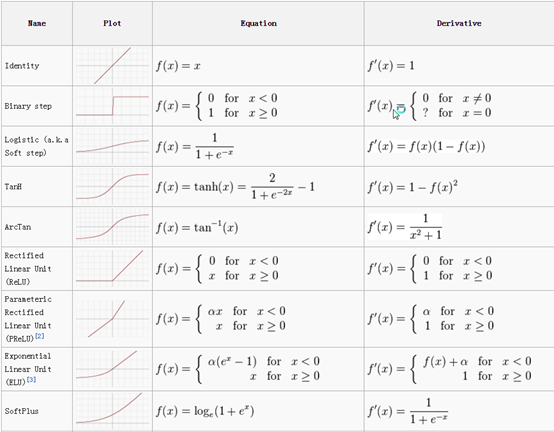
0x13 神经网络
前面介绍的神经元和激活函数是神经网络的基本构建,而一个神经网络由多个神经元构成,如下图:
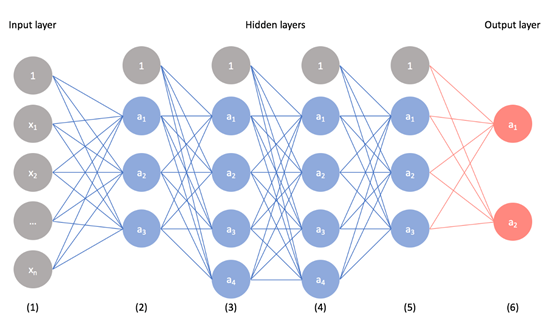
如上图,最左边的一层为输入层(Input Layer),这一层接收来自外界的输入,并将信号传递给下一层——Layer1,随后以此传递给Layer2-4,最后到达最右边的输出层(Output Layer)。而中间的Layer1-4我们把它们成为隐藏层(Hidden Layers),其中的数据无法在神经网络训练时观测到。上图中灰色的、独立于以上各层的单元叫做偏置单元(Bias Unit),具有调整函数信号传递的作用,从数学角度考虑,它是函数的截距。如函数 ,其中的n就是当 时的截距。网络层之间的信号也可以通过权值来调整。值得注意的是,隐藏层中的每一层的激活函数都可以有所不同,而神经网络的多样性正是由于神经网络中隐藏层的激活函数、网络层的权值、层数等的多样性而产生的。
0x20 卷积神经网络(CNN)
在神经网络中,卷积神经网络(CNN)是图像识别、图像分类重要分网络之一,对象检测、人脸识别等等都有CNN的影子。计算机将输入的图像视为像素阵列,然后根据图像分辨率(\(H \times W \times D\),其中H为高度,W为宽度,D为尺寸)生成不同的阵列图,如RGB彩色图像可生成为\(6\times6\times3\)(R,G,B各占一个尺寸)阵列或者\(4\times4\times1\)灰度图像阵列。
从CNN的过程来看,每个输入的图像通过滤波、池化、全连接等的处理,最后为了将这个神经网络输出的值量化成\([0,1]\)区间的概率值进行分类,引入了Softmax函数。下图是用CNN分类车辆图像的完整流程:

0x21 卷积层
在上图中的卷积层(Convolution Layer)是从输入图像中提取特征的第一层,实际上就是图像矩阵与卷积核或滤波器的卷积,这其实是一个数学计算过程。假设有一个5x5、像素值为0,1的图像与一个3x3的滤波器矩阵卷积,步长为1,如下图:

其卷积的过程如下图(图中的步骤不连续):
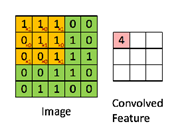

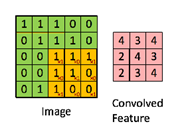
通过这一步骤,我们便可得到图像滤波后的特征,当然这只是简单的案例,真实的图像远比这种情复杂,需要考虑图像通道、图像分辨率、填充(Padding)方式、卷积核的设定等等。
0x22 池化层
池化层(也称为子采样或下采样)的作用是压缩卷积后产生的特征图的尺寸,它降低了每个特征的维度,但保留了更为重要的特征,池化层的类型可以是不同的,如:最大池化是选取特征矩阵中的最大值作为新的特征图;平均池化是取特征矩阵各个区域的平均值作为新的特征图;LP池化则通过取出特征矩阵各个区域中位数来计算特征图。如下图:
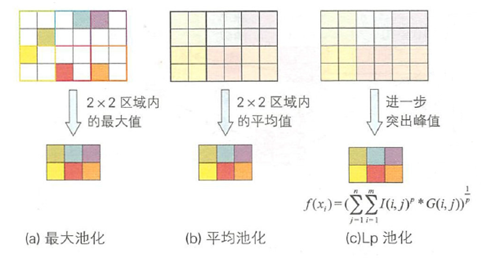
当然,池化层的类型绝不仅仅是以上三种,对于特殊用途的CNN有特殊的池化方式。
0x23 全连接层
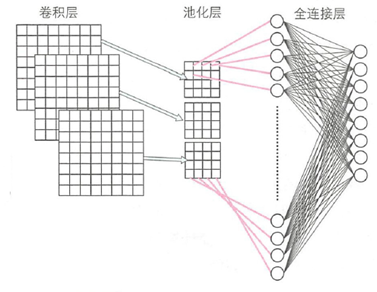
全连接层的作用是将来自卷积层或池化层输出的二维特征图降维。跟多层感知器一样,全连接层需要激活函数计算各个单元的输出值。虽然池化层与全连接层都有降维的目的,但与池化层不同的是,全连接层致力于把二维的特征矩阵转化为特征向量,如下图:
0x30 本章小结
本章重点介绍了神经网络的基础概念以及在数字图像处理较为常用的卷积神经网络,为下文降维融合的方法提供理论说明。